在excel中,可以使用很多公式,但是,有时候尽使用公式函数,是不能解决问题的,因为有的问题比较棘手,需要在借助公式的同时,还需要算法,推算出计算的算式,这样才能解决工作中的问题。下面,本例就带着大家一起来学习,在Excel中如何进行合成公式的推算!
下面我们先看这个表格,看下图。
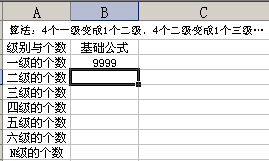
上图中,基本的理论依据是:每4个一级的材料就合成一个二级的材料;每4个二级就能合成一个三级的材料,同样的道理,每4个三级的,就能合成一个四级的材料……总之,每4个(N-1)级的材料能合成一个N级的材料。
现在,给出M个一级的材料,到底能合成多少个N级的材料。
根据上述的理论依据,我们可以逐级来合成,这样就能推算出最终的公式了。
看下图。要想从一级的个数中,合成多少个二级的,就得使用公式:=INT(B3/4)
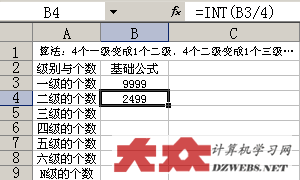
该公式的含义是:B3/4,其中,B3就是一级的个数,每四个合成一个二级的,拿这个数除以四取整数,就是二级的个数,因此,完整的公式为:=INT(B3/4)
同样的道理,二级的能合成多少个三级的,公式为::=INT(B4/4)
三级的合成四级的,公式为:=INT(B5/4),四级→五级公式为:=INT(B6/4);五级→六级:=INT(B7/4)……看如下公式,是五级的合成六级的。
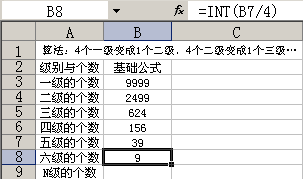
逐级合成的公式就给大家介绍到这里了,相信大家也明白,拿上一级的除以四再取整,就得到本级的个数,每一级都与4相关,但问题没这么简单,我们现在要推算的最终公式是:给出一级的个数M,任何时候都能直接推算出能合成多少个N级的。
下面再使用逐级总结的办法,就能推算出公式了。
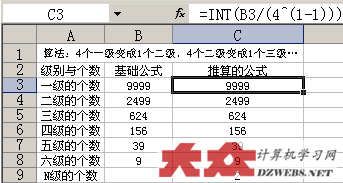
看上图,一级合成一级,自然是一个合成一个,公式为:=INT(B3/(4^(1-1)))
而一级合成二级的,公式为:=INT(B3/(4^(2-1))),看下图。
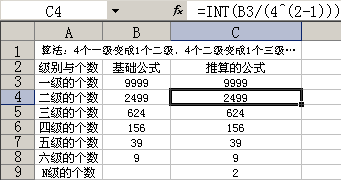
中间过程就不再过多阐述了,看最后的吧,如下图。
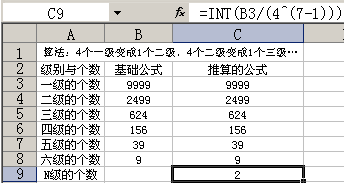
如果要直接合成7级的,那么,公式应为:=INT(B3/(4^(7-1)))。
如果你还不明白,那么,我们也可以给出完整的推算过程,假设M代表的就是一级的个数:
一级→二级公式为::=INT(M/(4^(2-1)))
二级→三级公式为::=INT(M/(4^(3-1)))
三级→四级公式为::=INT(M/(4^(4-1)))
四级→五级公式为::=INT(M/(4^(5-1)))
五级→六级公式为::=INT(M/(4^(6-1)))
六级→七级公式为::=INT(M/(4^(7-1)))
七级→八级公式为::=INT(M/(4^(8-1)))
…………
在Excel里面,上述公式中的4^(2-1)的含义是,4的(2-1)次方即4的1次方。现在,大家应该能看出了,公式里面出现的2,3,4,5,6,7,8代表的其实就是要转换的级数。而M则是一级的个数。所以,整个过程,仅与两个参数相关,即一级的个数和要转换的N级的数字。
因此,通用公式就是:=INT(M/(4^(N-1))),含义是:一级的个数M除以4的N减1次方。N就是要转换的级别。假设一级的个数为888888,要转换成为10级的,能得到多少个10级的?
此时,通用公式中,M等于888888,而N等于10,因此,=INT(M/(4^(N-1)))就变为:=INT(888888/(4^(10-1)))。这就是Excel中通过归纳推算出合成公式的简单例子。